Introducción completa a las estructuras de datos y algoritmos más esenciales

Anuncios

Estructuras de datos y algoritmos (DSA) a menudo se considera un tema intimidante, una creencia errónea común.

Al formar la base de los conceptos más innovadores en tecnología, son esenciales tanto en el viaje de los solicitantes de puestos de trabajo/pasantías como en el de los programadores experimentados.

Dominar DSA implica que puede usar su pensamiento computacional y algorítmico para resolver problemas nunca antes vistos y contribuir al valor de cualquier empresa de tecnología (¡incluida la suya!). Al comprenderlos, puede mejorar la capacidad de mantenimiento, la extensibilidad y la eficiencia de su código.

Te puede interesar también:

I. Estructuras de datos

arreglos
Listas vinculadas
pilas
Colas
Mapas y tablas hash
gráficos
Árboles
Árboles binarios y árboles de búsqueda binarios
Árboles autoequilibrados (Árboles AVL, Árboles Rojo-Negro, Árboles Splay)
Muchísimo
Intentos
Árboles de segmentos
Árboles Fenwick
Unión de conjuntos disjuntos
Árboles de expansión mínimos

II. Algoritmos

Divide y conquistaras
Algoritmos de clasificación (clasificación de burbujas, clasificación de conteo, clasificación rápida, clasificación de combinación, clasificación de Radix)
Algoritmos de búsqueda (búsqueda lineal, búsqueda binaria)
Tamiz de Eratóstenes
Algoritmo de Knuth-Morris-Pratt
Greedy I (Número máximo de intervalos no superpuestos en un eje)
Greedy II (Problema de la mochila fraccional)
Programación Dinámica I (0–1 Problema de Mochila)
Programación Dinámica II (Subsecuencia Común Más Larga)
Programación dinámica III (Subsecuencia creciente más larga)
Casco convexo
Gráficos transversales (búsqueda primero en amplitud, búsqueda primero en profundidad)
Algoritmo de Floyd-Warshall/Roy-Floyd
Algoritmo de Dijkstra y Algoritmo de Bellman-Ford
Clasificación topológica

I. Estructuras de datos

1. Matrices

Los arreglos son las estructuras de datos más simples y comunes. Se caracterizan por el fácil acceso a los elementos por índice (posición).

¿Para qué se usan?

Imagina tener una fila de sillas de teatro. Cada silla tiene asignada una posición (de izquierda a derecha), por lo que cada espectador tendrá asignado el número de la silla o sillas en las que se sentará. Esta es una matriz. ¡Expanda el problema a todo el teatro (filas y columnas de sillas) y tendrá una matriz 2D (matriz)!

Propiedades

los valores de los elementos se colocan en orden y se accede a ellos por su índice desde 0 hasta la longitud de la matriz-1;
una matriz es un bloque continuo de memoria;
suelen estar formados por elementos del mismo tipo (depende del lenguaje de programación);
el acceso y la adición de elementos son rápidos; la búsqueda y la eliminación no se realizan en O(1).

Enlaces útiles

2. Listas enlazadas

Las listas enlazadas son estructuras de datos lineales, al igual que las matrices. La principal diferencia entre las listas enlazadas y las matrices es que los elementos de una lista enlazada no se almacenan en ubicaciones de memoria contiguas. Se compone de nodos: entidades que almacenan el valor del elemento actual y una referencia de dirección al siguiente elemento. De esa manera, los elementos están vinculados por punteros.

¿Para qué se usan?

Una aplicación relevante de las listas enlazadas es la implementación de la página anterior y siguiente de un navegador. Una lista de doble enlace es la estructura de datos perfecta para almacenar las páginas mostradas por la búsqueda de un usuario.

Propiedades

vienen en tres tipos: simples, dobles y circulares;
los elementos NO se almacenan en un bloque contiguo de memoria;
perfecto para una excelente gestión de la memoria (el uso de punteros implica un uso dinámico de la memoria);
la inserción y la eliminación son rápidas; el acceso y la búsqueda de elementos se realizan en tiempo lineal.

Enlaces útiles

3. pilas

Una pila es un tipo de datos abstracto que formaliza el concepto de colección de acceso restringido. La restricción sigue la regla LIFO (Last In, First Out). Por lo tanto, el último elemento agregado en la pila es el primer elemento que elimina de ella.
Las pilas se pueden implementar usando arreglos o listas enlazadas.

¿Para qué se usan?

El ejemplo más común de la vida real utiliza platos colocados uno sobre otro en la cantina. La placa que está en la parte superior es la primera que se retira. El plato colocado más abajo es el que permanece en la pila durante más tiempo.
Una situación en la que las pilas son más útiles es cuando necesita obtener el orden inverso de los elementos dados. Simplemente empújelos todos en una pila y luego hágalos estallar.
Otra aplicación interesante es el problema de los paréntesis válidos. Dada una cadena de paréntesis, puede verificar que coincidan usando una pila.

Propiedades

solo puede acceder al último elemento a la vez (el que está en la parte superior);
una desventaja es que una vez que extrae elementos desde la parte superior para acceder a otros elementos, sus valores se perderán de la memoria de la pila;
el acceso de otros elementos se realiza en tiempo lineal; cualquier otra operación está en O(1).

Enlaces útiles

4. Colas

Una cola es otro tipo de datos de la colección de acceso restringido, al igual que la pila discutida anteriormente. La principal diferencia es que la cola está organizada según el modelo FIFO (primero en entrar, primero en salir): el primer elemento insertado en la cola es el primer elemento que se elimina. Las colas se pueden implementar mediante una matriz de longitud fija, una matriz circular o una lista enlazada.

¿Para qué se usan?

El mejor uso de este tipo de datos abstractos (ADT) es, por supuesto, la simulación de una cola de la vida real. Por ejemplo, en una aplicación de centro de llamadas, se usa una cola para guardar los clientes que están esperando recibir ayuda del consultor; estos clientes deben recibir ayuda en el orden en que llamaron.
Un tipo de cola especial y muy importante es la cola de prioridad. Los elementos se introducen en la cola en función de una “prioridad” asociada a ellos: el elemento con mayor prioridad es el primero que se introduce en la cola. Este ADT es esencial en muchos algoritmos gráficos (algoritmo de Dijkstra, BFS, algoritmo de Prim, codificación de Huffman, más sobre ellos a continuación). Se implementa mediante un montón.
Otro tipo especial de cola es la deque ( alerta de juego de palabras ).se pronuncia “cubierta”). Los elementos se pueden insertar/quitar de ambos extremos de la cola.

Propiedades

podemos acceder directamente solo al elemento “más antiguo” introducido;
la búsqueda de elementos eliminará todos los elementos accedidos de la memoria de la cola;
Hacer estallar/empujar elementos o ponerse al frente de la cola se realiza en tiempo constante. La búsqueda es lineal.

Enlaces útiles

5. Mapas y tablas hash

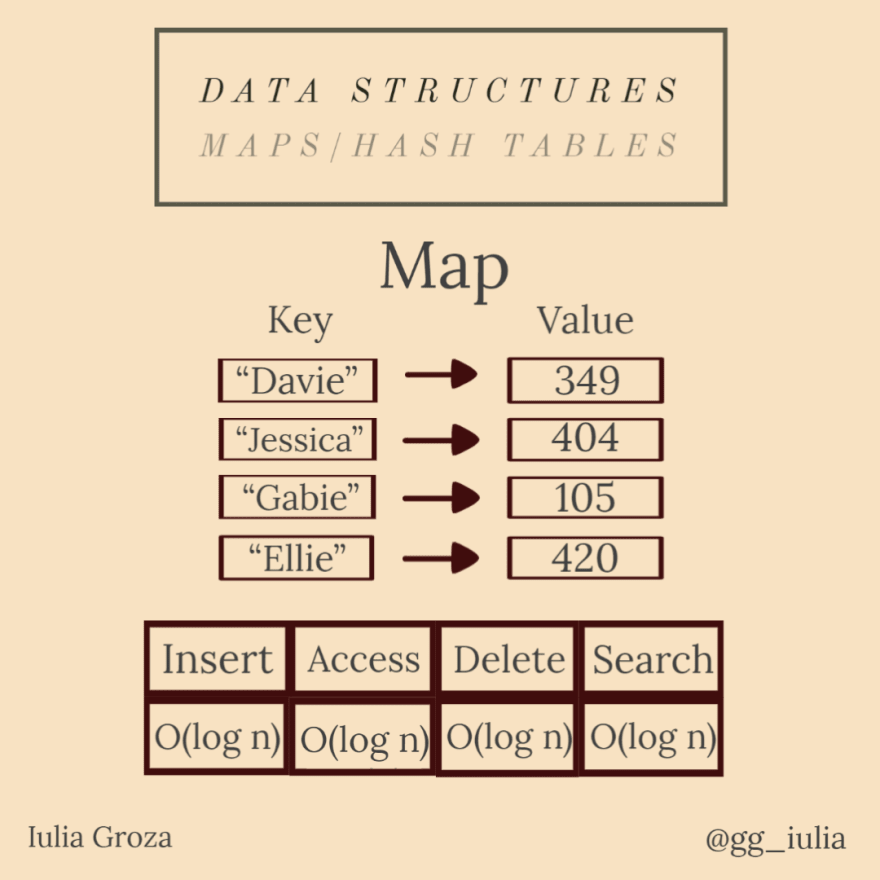
Los mapas (diccionarios) son tipos de datos abstractos que contienen una colección de claves y una colección de valores. Cada clave tiene un valor asociado.
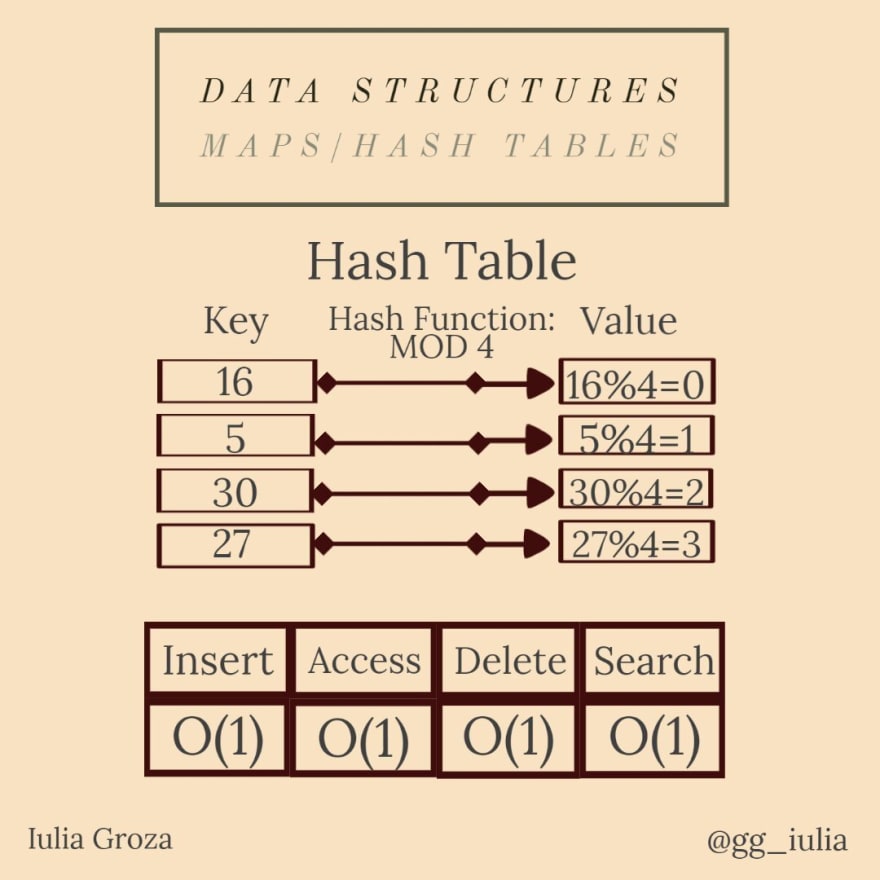
Una tabla hash es un tipo particular de mapa. Utiliza una función hash para generar un código hash, en una matriz de cubos o ranuras: la clave se codifica y el hash resultante indica dónde se almacena el valor.
La función hash más común (entre muchas) es la función de módulo constante. por ejemplo, si la constante es 6, el valor de la clave x es x%6 .
Idealmente, una función hash asignará cada clave a un cubo único, pero la mayoría de sus diseños emplean una función imperfecta, lo que podría conducir a la colisión entre claves con el mismo valor generado. Tales colisiones siempre se acomodan de alguna manera.

¿Para qué se usan?

La aplicación más conocida de los mapas es un diccionario de idiomas. Cada palabra de un idioma tiene asignada su definición. Se implementa mediante un mapa ordenado (sus claves están ordenadas alfabéticamente).
Contactos es también un mapa. Cada nombre tiene asignado un número de teléfono.
Otra aplicación útil es la normalización de valores. Digamos que queremos asignar a cada minuto de un día (24 horas = 1440 minutos) un índice de 0 a 1439. La función hash será h(x) = x.hora*60+x.minuto .

Propiedades

las claves son únicas (sin duplicados);
resistencia a la colisión: debería ser difícil encontrar dos entradas diferentes con la misma tecla;
resistencia pre-imagen: dado un valor H, debería ser difícil encontrar una clave x, tal que h(x)=H ;
segunda resistencia previa a la imagen: dada una clave y su valor, debería ser difícil encontrar otra clave con el mismo valor;
terminología:
* “mapa”: Java, C++;
* “diccionario”: Python, JavaScript, .NET;
* “matriz asociativa”: PHP.
debido a que los mapas se implementan utilizando árboles rojo-negro autoequilibrados (se explica a continuación), todas las operaciones se realizan en O (log n); todas las operaciones de la tabla hash son constantes.

Enlaces útiles

Conjunto de problemas de Codeforces

6. Gráficos

Un gráfico es una estructura de datos no lineal que representa un par de dos conjuntos: G={V, E} , donde V es el conjunto de vértices (nodos) y E el conjunto de aristas (flechas). Los nodos son valores interconectados por bordes: líneas que representan la dependencia (a veces asociada con un costo/distancia) entre dos nodos.
Hay dos tipos principales de grafos: dirigidos y no dirigidos. En un gráfico no dirigido, el borde (x, y) está disponible en ambas direcciones: (x, y) y (y, x) . En un gráfico dirigido, la arista (x, y) se llama flecha y la dirección viene dada por el orden de los vértices en su nombre: flecha (x, y) es diferente de flecha (y, x) .

¿Para qué se usan?

Los gráficos son la base de todo tipo de red: una red social (como Facebook, LinkedIn), o incluso la red de calles de una ciudad. Cada usuario de una plataforma de redes sociales es una estructura que contiene todos sus datos personales: representa un nodo de la red. Las amistades en Facebook son aristas en una gráfica no dirigida (porque es recíproca), mientras que en Instagram o Twitter, la relación entre una cuenta y sus seguidores/cuentas siguientes son flechas en una gráfica dirigida (no recíproca).

Propiedades

La teoría de grafos es un dominio amplio, pero vamos a destacar algunos de los conceptos más conocidos:

el grado de un nodo en un grafo no dirigido es el número de sus aristas incidentes;
el grado interno/externo de un nodo en un gráfico dirigido es el número de flechas que dirigen hacia/desde ese nodo;
una cadena desde el nodo x hasta el nodo y es una sucesión de aristas adyacentes, con x como su extremo izquierdo e y como su extremo derecho;
un ciclo es una cadena donde x=y; un gráfico puede ser cíclico/acíclico; un grafo es conexo si hay una cadena entre dos nodos cualesquiera de V;
un gráfico puede recorrerse y procesarse utilizando Breadth First Search (BFS) o Depth First Search (DFS), ambos realizados en O(|V|+|E|), donde |S| es el cardinal del conjunto S; Consulte los enlaces a continuación para obtener otra información esencial en la teoría de grafos.

Enlaces útiles

7. árboles

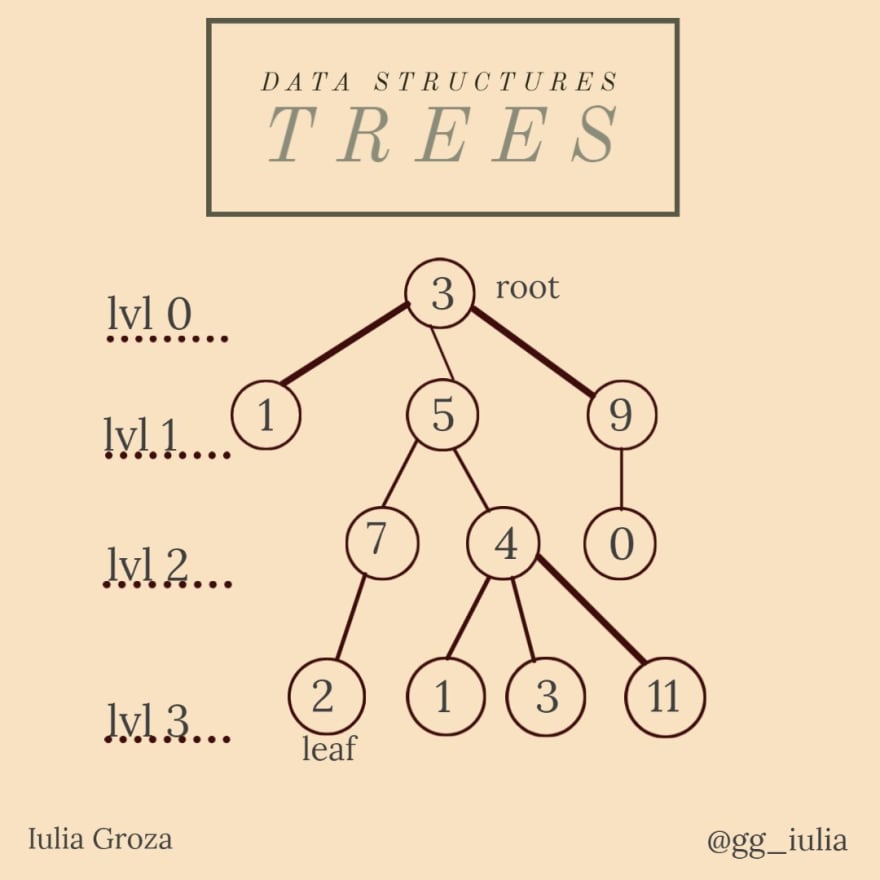
Un árbol es un gráfico no dirigido, mínimo en términos de conectividad (si eliminamos un solo borde, el gráfico ya no estará conectado) y máximo en términos de aciclicidad (si agregamos un solo borde, el gráfico ya no será acíclico) . Entonces, cualquier gráfico no dirigido conectado acíclico es un árbol, pero para simplificar, nos referiremos a los árboles con raíces como árboles.
Una raíz es un nodo fijo que establece la dirección de los bordes en el árbol, así que ahí es donde “comienza” todo. Las hojas son los nodos terminales del árbol, ahí es donde “termina” todo.
Un hijo de un vértice es su vértice incidente debajo de él. Un vértice puede tener varios hijos. El padre de un vértice es su vértice incidente sobre él: es único.

¿Para qué se usan?

Usamos árboles cada vez que debemos representar una jerarquía. Nuestro propio árbol genealógico es el ejemplo perfecto. Tu antepasado más antiguo es la raíz del árbol. La generación más joven representa el conjunto de hojas.
Los árboles también pueden representar la relación de subordinación en la empresa para la que trabaja. De esa manera, puede averiguar quién es su gerente y a quién debe administrar.

Propiedades

la raíz no tiene padre;
las hojas no tienen hijos;
la longitud de la cadena entre la raíz y un nodo x representa el nivel en el que se encuentra x;
la altura de un árbol es el nivel máximo del mismo (3 en nuestro ejemplo);
el método más común para recorrer un árbol es DFS en O(|V|+|E|), pero también podemos usar BFS; el orden de los nodos recorridos en cualquier gráfico usando DFS forman el árbol DFS que nos indica el tiempo que se ha visitado un nodo.

Enlaces útiles

8. Árboles binarios y árboles de búsqueda binarios

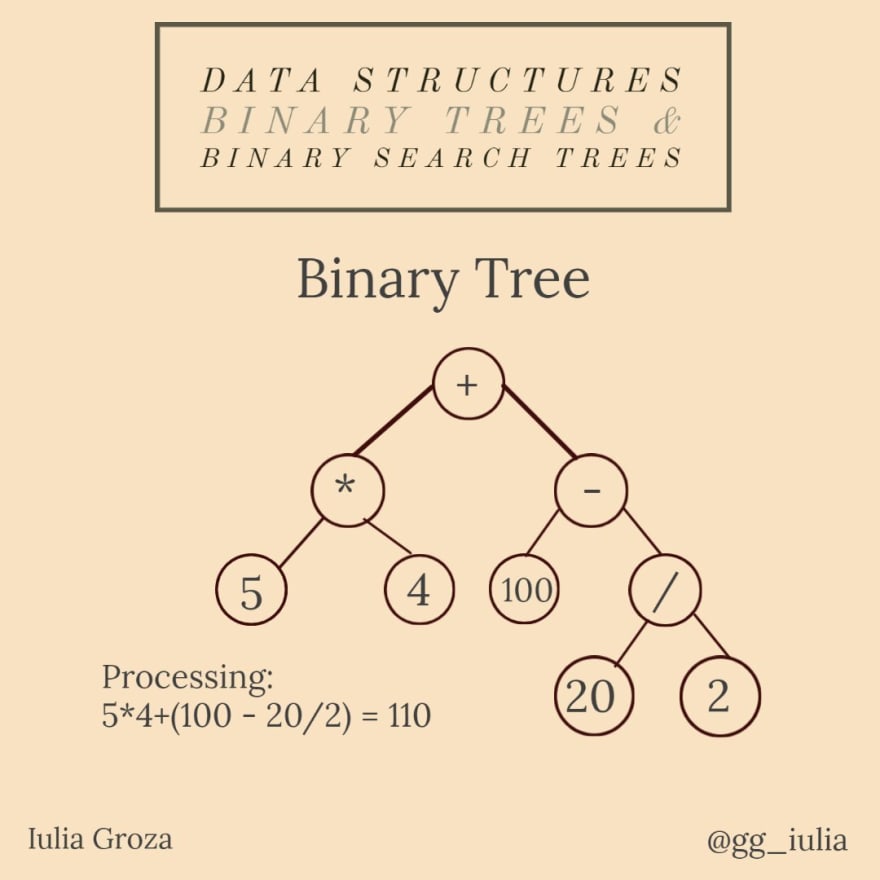
Un árbol binario es un tipo especial de árbol: cada vértice puede tener un máximo de dos hijos. En un árbol binario estricto, cada nodo tiene exactamente dos hijos, excepto las hojas. Un árbol binario completo con n niveles tiene todos los 2ⁿ-1 nodos posibles.
Un árbol de búsqueda binario es un árbol binario donde los valores de los nodos pertenecen a un conjunto totalmente ordenado: el valor de cualquier nodo elegido arbitrariamente es mayor que todos los valores del subárbol izquierdo y menor que los del subárbol derecho.

¿Para qué se usan?

Una aplicación importante de BT es la representación y evaluación de expresiones lógicas. Cada expresión se puede descomponer en variables/constantes y operadores. Este método de escritura de expresiones se llama notación polaca inversa (RPN). De esa manera, pueden formar un árbol binario, donde los nodos internos son operadores y las hojas son variables/constantes; se llama árbol de sintaxis abstracta (AST).
Los BST se utilizan con frecuencia debido a su rápida búsqueda de propiedades de claves. Los árboles AVL, los árboles rojo-negro, los conjuntos ordenados y los mapas se implementan mediante BST.

Propiedades

Hay tres tipos de recorridos DFS para BT:
* Pedido anticipado (Raíz, Izquierda, Derecha);
* En orden (Izquierda, Raíz, Derecha);
* Posorden (Izquierda, Derecha, Raíz); todo hecho en tiempo O(n);
el recorrido en orden nos da todos los nodos en el árbol en orden ascendente;
el nodo más a la izquierda es el valor mínimo en el BST y el más a la derecha es el máximo;
observe que RPN es el recorrido en orden del AST;
un BST tiene las ventajas de una matriz ordenada, pero la desventaja de la inserción logarítmica: todas sus operaciones se realizan en tiempo O (log n).

Enlaces útiles

9. Árboles autoequilibrados

Todos estos tipos de árboles son árboles de búsqueda binarios autoequilibrados. La diferencia está en la forma en que equilibran su altura en tiempo logarítmico.
Los árboles AVL se autoequilibran después de cada inserción/eliminación porque la diferencia de módulo entre las alturas del subárbol izquierdo y el subárbol derecho de un nodo es un máximo de 1. Los AVL llevan el nombre de sus inventores: Adelson-Velsky y Landis.
En Red-Black Trees, cada nodo almacena un bit adicional que representa el color, que se utiliza para garantizar el equilibrio después de cada operación de inserción/eliminación.
En los árboles Splay, los nodos a los que se accedió recientemente se pueden volver a acceder rápidamente, por lo que la complejidad del tiempo amortizado de cualquier operación sigue siendo O (log n).

¿Para qué se usan?

Un AVL parece ser la mejor estructura de datos en la teoría de bases de datos.
Los RBT se utilizan para organizar piezas de datos comparables, como fragmentos de texto o números. En la versión 8 de Java, los HashMaps se implementan mediante RBT. Las estructuras de datos en geometría computacional y programación funcional también se construyen con RBT.
Los árboles de distribución se utilizan para cachés, asignadores de memoria, recolectores de basura, compresión de datos, cuerdas (reemplazo de la cadena utilizada para cadenas de texto largas), en Windows NT (en la memoria virtual, la red y el código del sistema de archivos).

Propiedades

la complejidad del tiempo amortizado de CUALQUIER operación en CUALQUIER BST autoequilibrado es O(log n);
la altura máxima de un AVL en el peor de los casos es 1.44 * log2n (¿Por qué? *pista: piense en el caso de un AVL con todos los niveles llenos, excepto el último que tiene un solo elemento);
Los AVL son los más rápidos en la práctica para buscar elementos, pero la rotación de subárboles para el autoequilibrio es costosa;
mientras tanto, los RBT proporcionan inserciones y eliminaciones más rápidas porque no hay rotaciones;
Los árboles de distribución no necesitan almacenar ningún dato de contabilidad.

Enlaces útiles

10. montones

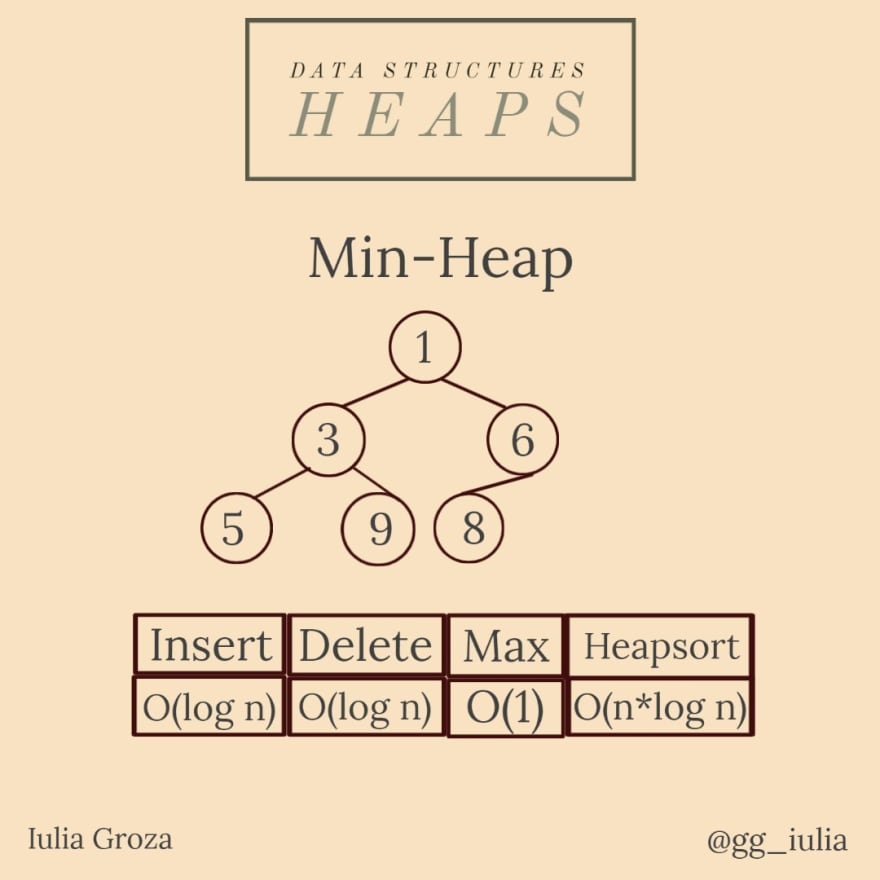
Un montón mínimo es un árbol binario donde cada nodo tiene la propiedad de que su valor es mayor o igual que el valor de su padre: val[par[x]] <= val[x] , con un nodo xa del montón, donde val[ x] es su valor y par[x] su padre.
También hay un montón máximo que implementa la relación opuesta.
Un montón binario es un árbol binario completo (todos sus niveles están llenos, excepto quizás el último nivel).

¿Para qué se usan?

Como lo discutimos unos días antes, las colas de prioridad se pueden implementar de manera eficiente utilizando un montón binario porque admite las operaciones de inserción (), eliminar (), extraer Max () y disminuir la clave () en tiempo O (log n). De esa manera, los montones también son esenciales en los algoritmos gráficos (debido a la cola de prioridad).
Cada vez que necesite un acceso rápido al elemento máximo/mínimo, la mejor opción es un montón.
Los montones también son la base del algoritmo heapsort.

Propiedades

siempre está equilibrado: cada vez que eliminamos/insertamos un elemento en la estructura, solo tenemos que “tamizar”/”percolar” hasta que esté en la posición correcta;
el padre de un nodo k > 1 es [k/2] (donde [x] es la parte entera de x) y sus hijos son 2*ky 2 *k+1 ;
se establece una alternativa de una cola de prioridad, order_map (en C++) o cualquier otra estructura ordenada que pueda permitir fácilmente el acceso al elemento mínimo/máximo;
se prioriza la raíz, por lo que la complejidad temporal de su acceso es O(1), la inserción/eliminación se realiza en O(log n); la creación de un montón se realiza en O(n); heapsort en O(n*log n).

Enlaces útiles

GeeksforGeeks: Montones

11.Intentos

Un trie es una estructura de datos de recuperación de información eficiente. También conocido como árbol de prefijos, es un árbol de búsqueda que permite insertar y buscar en complejidad de tiempo O(L), donde L es la longitud de la clave.
Si almacenamos claves en un BST bien equilibrado, necesitará un tiempo proporcional a L * log n, donde n es el número de claves en el árbol. De esa manera, un trie es una estructura de datos mucho más rápida (con O (L)) en comparación con un BST, pero la penalización está en los requisitos de almacenamiento de trie.

¿Para qué se usan?

Un trie se usa principalmente para almacenar cadenas y sus valores. Una de sus aplicaciones más geniales es escribir autocompletar y autosugerencias en la barra de búsqueda de Google. Un trie es la mejor opción porque es la opción más rápida: una búsqueda más rápida es más valiosa que el almacenamiento ahorrado si no usamos un trie.
La autocorrección ortográfica de las palabras escritas también se realiza mediante un trie, buscando la palabra en el diccionario o tal vez buscando otras instancias en el mismo texto.

Propiedades

tiene una asociación clave-valor; la clave suele ser una palabra o un prefijo de la misma, pero puede ser cualquier lista ordenada;
la raíz tiene una cadena vacía como clave;
la diferencia de longitud entre el valor de un nodo y los valores de sus hijos es 1; de esa forma, los hijos de la raíz almacenarán un valor de longitud 1; como conclusión podemos decir que un nodo x de un nivel k tiene un valor de longitud k;
como hemos dicho, la complejidad temporal de las operaciones de inserción/búsqueda es O(L), donde L es la longitud de la clave, que es mucho más rápida que la O(log n) de un BST, pero comparable a una tabla hash;
la complejidad del espacio es en realidad una desventaja: O(ALPHABET_SIZE*L*n).

Enlaces útiles

12. Segmentar árboles

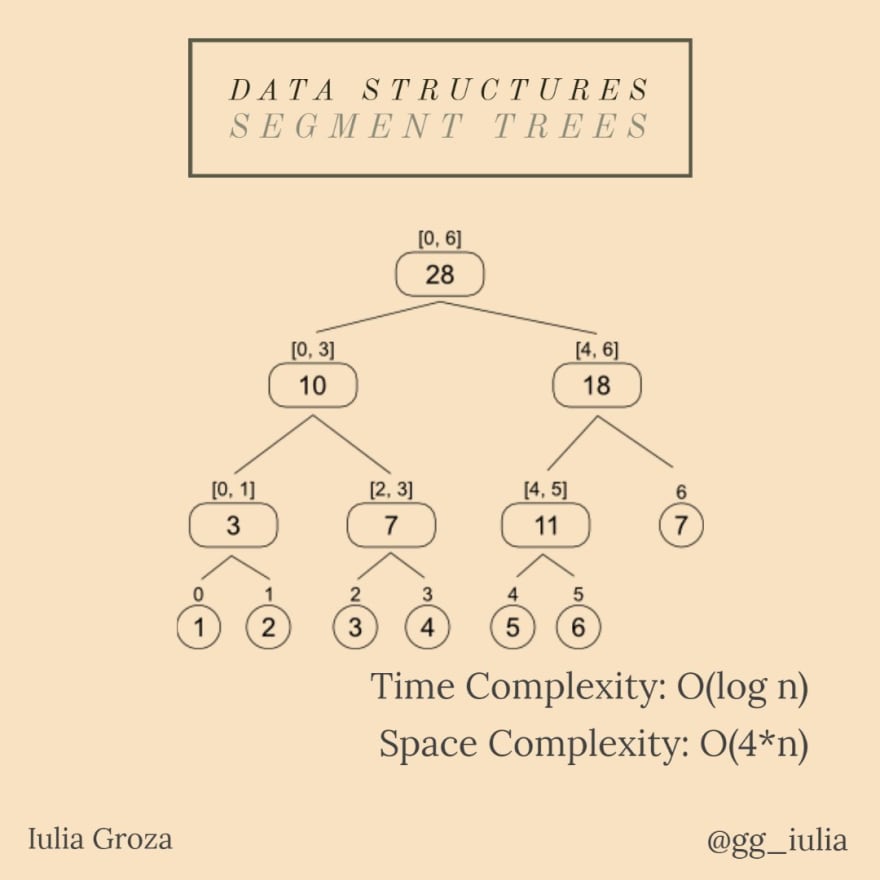
Un árbol de segmentos es un árbol binario completo que permite responder a las consultas de manera eficiente, al mismo tiempo que modifica fácilmente sus elementos.
Cada elemento en el índice i en la matriz dada representa una hoja etiquetada con el intervalo [i, i] . Un nodo que tenga sus hijos etiquetados [x, y] , respectivamente [y, z] , tendrá el intervalo [x, z] como etiqueta. Por lo tanto, dados n elementos (indexados en 0), la raíz del árbol de segmentos se etiquetará con [0, n-1] .

¿Para qué se usan?

Son extremadamente útiles en tareas que se pueden resolver usando Divide & Conquer (primer concepto de algoritmos que vamos a discutir) y también pueden requerir actualizaciones en sus elementos. De esa forma, al actualizar el elemento, también se modifica cualquier intervalo que lo contenga, por lo que la complejidad es logarítmica. Por ejemplo, la suma/máximo/mínimo de n elementos dados son las aplicaciones más comunes de los árboles de segmentos. La búsqueda binaria también puede usar un árbol de segmentos si se están produciendo actualizaciones de elementos.

Propiedades

siendo un árbol binario, un nodo x tendrá 2*x y 2*x+1 como hijos y [x/2] como padre, donde [x] es la parte entera de x;
un método eficiente para actualizar un rango completo en un árbol de segmentos se llama “Propagación diferida” y también se realiza en O (log n) (consulte los enlaces a continuación para la implementación de las operaciones);
pueden ser k-dimensionales: por ejemplo, teniendo q consultas para encontrar la suma de las submatrices dadas de una matriz, podemos usar un árbol de segmentos de 2 dimensiones;
la actualización de elementos/rango requiere tiempo O(log n); responder a una consulta es constante (O(1));
la complejidad del espacio es lineal, lo cual es una GRAN ventaja: O(4*n).

Enlaces útiles

13. Árboles Fenwick

Un árbol fenwick, también conocido como árbol indexado binario (BIT), es una estructura de datos que también se utiliza para actualizaciones y consultas eficientes. En comparación con los árboles de segmentos, los BIT requieren menos espacio y son más fáciles de implementar.

¿Para qué se usan?

Los BIT se utilizan para calcular sumas de prefijos: la suma de prefijos del elemento en la i-ésima posición es la suma de los elementos desde la primera posición hasta la i-ésima. Se representan mediante una matriz, donde cada índice se representa en el sistema binario. Por ejemplo, un índice 10 es equivalente a un índice 2 en el sistema decimal.

Propiedades

la construcción del árbol es la parte más interesante: en primer lugar, la matriz debe estar indexada en 1; para encontrar el padre del nodo x, debe convertir su índice x al sistema binario y voltear el bit más significativo a la derecha; ex. el padre del nodo 6 es 4; 6 = 1*2²+1*2¹+0*2⁰ => 1″1″0 (voltear)=> 100 = 1*2²+0*2¹+0*2⁰ = 4 ;
finalmente, elementos ANDing, cada nodo debe contener un intervalo que se puede agregar a la suma del prefijo (más sobre la construcción e implementación en los enlaces a continuación);
la complejidad del tiempo sigue siendo O(log n) para las actualizaciones y O(1) en las consultas, pero la complejidad del espacio es una ventaja aún mayor: O(n), en comparación con el O(4*n) del árbol de segmentos.

Enlaces útiles

14. Unión de conjuntos disjuntos

Nos dan n elementos, cada uno de ellos representando un conjunto separado. Disjoint Set Union (DSU) nos permite hacer dos operaciones:

UNION: combina dos conjuntos (o unifica los conjuntos de dos elementos diferentes si no son del mismo conjunto);
ENCONTRAR: encuentra el conjunto del que proviene un elemento.

¿Para qué se usan?

Las DSU son muy importantes en la teoría de grafos. Podría verificar si dos vértices provienen del mismo componente conectado o incluso unificar dos componentes conectados.
Tomemos el ejemplo de las ciudades y los pueblos. Dado que las ciudades vecinas con crecimiento demográfico y económico se están expandiendo, pueden crear fácilmente una metrópoli. Por lo tanto, se combinan dos ciudades y sus residentes viven en la misma metrópoli. También podemos comprobar en qué ciudad vive una persona llamando a la función FIND.

Propiedades

se representan utilizando árboles; una vez que se combinan dos conjuntos, una de las dos raíces se convierte en la raíz principal y el padre de la otra raíz es una de las hojas del otro árbol;
un tipo de optimización práctica es la compresión de árboles por su altura; de esa manera, la unión se realiza mediante el árbol más grande para actualizar fácilmente los datos de ambos (consulte la implementación a continuación);
todas las operaciones se realizan en tiempo O(1).

Enlaces útiles

15. Árboles de expansión mínimos

Dado un grafo conectado y no dirigido, un árbol de expansión de ese grafo es un subgrafo que es un árbol y conecta todos los nodos. Un solo gráfico puede tener muchos árboles de expansión diferentes. Un árbol de expansión mínimo (MST) para un gráfico ponderado, conectado y no dirigido es un árbol de expansión con un peso (costo) menor o igual que el peso de cualquier otro árbol de expansión. El peso de un árbol de expansión es la suma de los pesos asignados a cada borde del árbol de expansión.

¿Para qué se usan?

El problema MST es un problema de optimización, un problema de costo mínimo. Al tener una red de rutas, podemos considerar que uno de los factores que influyen en el establecimiento de una ruta nacional entre n ciudades es la distancia mínima entre dos ciudades adyacentes.
De esa forma, la ruta nacional está representada por el MST del gráfico de la red vial.

Propiedades

siendo un árbol, un MST de un grafo con n vértices tiene n-1 aristas; se puede resolver usando:
* Algoritmo de Prim: la mejor opción para gráficos densos (gráficos con n nodos y el número de aristas es cercano a n(n-1)/2 );
* Algoritmo de Kruskal: se usa principalmente; es un algoritmo Greedy basado en Disjoint Set Union (también lo discutiremos);
la complejidad temporal de su construcción es O(n log n) u O(n log m) para Kruskal (depende del gráfico) y O(n²) para Prim.

Enlaces útiles

II. Algoritmos

1. Divide y vencerás

Divide and Conquer (DAC) no es un algoritmo específico en sí mismo, sino una categoría importante de algoritmos que debe entenderse antes de profundizar en otros temas. Se utiliza para resolver problemas que se pueden dividir en subproblemas que son similares al problema original, pero de menor tamaño. Luego, DAC los resuelve recursivamente y finalmente combina los resultados para encontrar la solución del problema.
Tiene tres etapas:

Dividir — los problemas en subproblemas;
Conquistar — los subproblemas usando la recursividad;
Combinar: los resultados de los subproblemas en la solución final.

¿Para qué se usa esto?

Una aplicación práctica de DAC es la programación en paralelo utilizando múltiples procesadores, por lo que los subproblemas se ejecutan en diferentes máquinas.
DAC es la base de muchos algoritmos como Quick Sort, Merge Sort, Binary Search o algoritmos de multiplicación rápida.

Propiedades

cada problema DAC se puede escribir como una relación de recurrencia; entonces, es esencial encontrar el caso básico que detenga la recursividad;
su complejidad es T(n)=D(n)+C(n)+M(n) , lo que significa que cada etapa tiene una complejidad diferente dependiendo del problema.

Enlaces útiles

2. Algoritmos de clasificación

Se utiliza un algoritmo de clasificación para reorganizar elementos dados (de una matriz o lista) de acuerdo con un operador de comparación en los elementos. Cuando nos referimos a una matriz ordenada, generalmente pensamos en orden ascendente (el operador de comparación es ‘<‘). Hay varios tipos de clasificación, con diferentes complejidades de tiempo y espacio. Algunos de ellos están basados en la comparación, otros no. Estos son los métodos de clasificación más populares/eficientes:

Ordenamiento de burbuja

Bubble Sort es uno de los algoritmos de clasificación más simples. Se basa en un intercambio repetido entre elementos adyacentes si están en un orden incorrecto. Es estable, su complejidad temporal es O(n²) y necesita espacio auxiliar O(1).

Anuncios

Visualización de clasificación de burbujas

Clasificación de conteo

Counting Sort no es una clasificación basada en la comparación. Básicamente, utiliza la frecuencia de cada elemento (una especie de hashing), determina el valor mínimo y máximo y luego itera entre ellos para colocar cada elemento en función de su frecuencia. Se hace en O(n) y el espacio es proporcional al rango de datos. Es eficiente si el rango de entrada no es significativamente mayor que el número de elementos.

Visualización de clasificación de conteo

Ordenación rápida

Quick Sort es una aplicación de Divide and Conquer. Se basa en elegir un elemento como pivote (primero, último o mediano) y luego intercambiar elementos para colocar el pivote entre todos los elementos más pequeños que él y todos los elementos más grandes que él. No tiene espacio adicional ni complejidad de tiempo O(n*log n), la mejor complejidad para los métodos basados en la comparación.
Aquí hay una demostración con la elección del pivote como el último elemento:

Visualización de clasificación rápida

Ordenar por fusión

Merge Sort también es una aplicación Divide & Conquer. Divide la matriz en dos mitades, ordena cada mitad y luego las fusiona. Su complejidad de tiempo también es O(n*log n), por lo que también es súper rápido como Quick Sort, pero desafortunadamente necesita O(n) espacio adicional para almacenar dos subarreglos al mismo tiempo y, finalmente, fusionarlos.

Combinación de clasificación de visualización

Clasificación Radix

Radix Sort usa Counting Sort como una subrutina, por lo que no es un algoritmo basado en comparación. ¿Cómo sabemos que CS no es suficiente? Supongamos que tenemos que ordenar elementos en [1, n²] . Usando CS, nos llevaría O(n²). Necesitamos un algoritmo lineal: O(n+k), donde los elementos están en el rango [1, k] . Ordena los elementos dígito a dígito comenzando por el menos significativo (unidades), hasta el más significativo (decenas, centenas, etc.). Espacio adicional (de CS): O(n).

Visualización de clasificación Radix

Enlaces útiles

3. Algoritmos de búsqueda

Los algoritmos de búsqueda están diseñados para verificar la existencia de un elemento en una estructura de datos e incluso devolverlo. Hay un par de métodos de búsqueda, pero estos son los dos más populares:

Búsqueda lineal

El enfoque de este algoritmo es muy simple: comienza a buscar su valor desde el primer índice de la estructura de datos. Los compara uno por uno hasta que su valor y su elemento actual sean iguales. Si ese valor específico no está en el DS, devuelve -1.
Complejidad de tiempo: O(n)

Búsqueda binaria

BS es un algoritmo de búsqueda eficiente basado en Divide and Conquer. Desafortunadamente, solo funciona en estructuras de datos ordenadas. Al ser un método DAC, divide continuamente el DS en dos mitades y compara su valor de búsqueda con el valor del elemento central. Si son iguales, la búsqueda ha terminado. De cualquier manera, si su valor es mayor/menor que este, la búsqueda debería continuar en la mitad derecha/izquierda.
Complejidad de tiempo: O (log n)

Enlaces útiles

4. Tamiz de Eratóstenes

Dado un número entero n, imprime todos los números primos menores o iguales a n.
Sieve of Eratosthenes es uno de los algoritmos más eficientes que resuelve este problema y funciona perfectamente para n menor que 10.000.000 .
El método utiliza una lista/mapa de frecuencias que marca la primalidad de cada número en el rango [0, n] : ok[x]=0 si x es primo, ok[x]=1 en caso contrario.

Comenzamos eligiendo cada número primo de nuestra lista y marcando sus múltiplos de la lista con 1; de esa manera, elegimos los números sin marcar (0). Finalmente, podemos responder fácilmente en O(1) a tantas consultas como queramos.

El algoritmo clásico es esencial en muchas aplicaciones, pero hay algunas optimizaciones que podemos hacer. En primer lugar, podemos notar fácilmente que 2 es el único número primo par, por lo que podemos verificar sus múltiplos por separado y luego iterar en el rango para encontrar números primos de dos a dos. En segundo lugar, es obvio que para un número x, previamente habíamos verificado 2x, 3x, 4x, etc. cuando iterábamos a través de 2, 3, etc. De esa manera, nuestro bucle for de verificación múltiple puede comenzar desde x² cada vez. Finalmente, incluso la mitad de estos múltiplos son pares y también estamos iterando a través de números primos impares, por lo que podemos iterar fácilmente desde 2*x hasta 2*x en el ciclo de verificación de múltiplos.

Complejidad espacial: O(n)
Complejidad temporal: O(n*log(log n)) para el algoritmo clásico, O(n) para el optimizado.
¿Por qué O(n*log(log n))?
La respuesta

Enlaces útiles

Tamiz de la implementación de Eratóstenes

5. Algoritmo de Knuth-Morris-Pratt

Dado un texto de longitud n y un patrón de longitud m, encuentre todas las ocurrencias del patrón en el texto.
El algoritmo Knuth-Morris-Pratt (KMP) es una forma eficiente de resolver el problema de coincidencia de patrones.
La solución ingenua se basa en usar una “ventana deslizante”, donde comparamos carácter a carácter cada vez que establecemos un nuevo índice de inicio, comenzando desde el índice 0 del texto hasta el índice nm. De esa forma, la complejidad del tiempo es O(m*(n-m+1))~O(n*m).
KMP es una optimización de la solución ingenua: se realiza en O(n) y funciona mejor cuando el patrón tiene muchos subpatrones repetidos. Por lo tanto, también utiliza una ventana deslizante, pero en lugar de comparar todos los caracteres con los de la subcadena, busca constantemente el sufijo más largo del subpatrón actual, que también es su prefijo. En otras palabras, cada vez que detectamos una falta de coincidencia después de algunas coincidencias, ya conocemos algunos de los caracteres en el texto de la siguiente ventana. Por lo tanto, es inútil volver a emparejarlos, por lo que reiniciamos la coincidencia con el mismo carácter en el texto con un carácter después de ese prefijo. ¿Cómo sabemos cuántos caracteres debemos omitir? Bueno, deberíamos crear una matriz de preprocesamiento que nos diga cuántos caracteres se deben omitir.

Enlaces útiles

6. Greedy

El método Greedy se usa principalmente para problemas que requieren optimización y la solución óptima local conduce a la solución óptima global.
Dicho esto, al usar Greedy, la solución óptima en cada paso conduce a la solución óptima general. Sin embargo, en la mayoría de los casos, la decisión que tomamos en un paso afecta la lista de decisiones para el siguiente paso. En este caso, el algoritmo debe demostrarse matemáticamente. Greedy también produce excelentes soluciones en algunos problemas matemáticos, pero no en todos (¡es posible que la solución más óptima no esté garantizada)!

Un algoritmo Greedy generalmente tiene cinco componentes:

un conjunto de candidatos, a partir del cual se crea una solución;
una función de selección: elige al mejor candidato;
una función de viabilidad: puede determinar si un candidato puede contribuir a la solución;
una función objetiva: asigna el candidato a la solución (parcial);
una función de solución: construye la solución a partir de las soluciones parciales.

Problema de la mochila fraccionada

Dados los pesos y valores de n artículos, necesitamos poner estos artículos en una mochila de capacidad W para obtener el máximo valor total en la mochila (se permite tomar piezas de artículos: el valor de una pieza es proporcional a su peso).

La idea básica del enfoque codicioso es clasificar todos los artículos en función de su relación valor/peso. Luego, podemos agregar tantos elementos completos como podamos. En el momento en que encontremos un artículo más pesado (w2) que nuestro peso disponible que queda en la mochila (w1), lo fraccionaremos: tomaremos solo w2-w1 para maximizar nuestra ganancia. Se garantiza que esta solución codiciosa es correcta.

Enlaces útiles

7. Programación dinámica

La programación dinámica (DP) es un enfoque similar a Divide & Conquer. También divide el problema en subproblemas similares, pero en realidad se superponen y son codependientes, no se resuelven de forma independiente.

El resultado de cada subproblema se puede usar en cualquier momento posterior y se construye usando memorización (cálculo previo). DP se usa principalmente para la optimización (tiempo y espacio) y se basa en encontrar una recurrencia.

Las aplicaciones de DP incluyen la serie de números de Fibonacci, la Torre de Hanoi, Roy-Floyd-Warshall, Dijkstra, etc. A continuación, analizaremos una solución de DP del problema de la mochila 0-1.

0–1 Problema de mochila

Dados los pesos y valores de n artículos, necesitamos poner estos artículos en una mochila de capacidad W para obtener el valor total máximo en la mochila (no se permite el fraccionamiento de artículos como en la solución Greedy).
La propiedad 0-1 viene dada por el hecho de que debemos elegir todo el elemento o no elegirlo en absoluto.
Construimos una estructura DP como una matriz dp[i][cw] que almacena la máxima ganancia que podemos obtener eligiendo i objetos cuyo peso total sea cw. Es fácil notar que primero debemos inicializar dp[1][w[i]] con v[i] , donde w[i] es el peso del i-ésimo objeto y v[i] su valor.
La recurrencia es la siguiente:dp[i][cw] = max(dp[i-1][cw], dp[i-1][cw-w[i]]+v[i]) . Analicémoslo un poco.
dp[i-1][cw] representa el caso en el que no agregamos el elemento actual en la mochila. dp[i-1][cw-w[i]]+v[i] es el caso en el que añadimos el elemento. Dicho esto, dp[i-1][cw-w[i]] es el beneficio máximo de tomar elementos i-1: por lo que su peso es el peso actual sin el peso de nuestro artículo.

Finalmente, le agregamos el valor de nuestro artículo.
La respuesta se almacena en dp[n][W]. Se realiza una optimización con una simple observación: en la recurrencia, la línea actual (fila) está influenciada solo por la línea anterior. Por lo tanto, no es necesario almacenar la estructura de DP en una matriz, por lo que debemos elegir una matriz para una mejor complejidad espacial: O(n). Complejidad temporal: O(n*W).

Enlaces útiles

0–1 Implementación del problema de la mochila

8. Subsecuencia común más larga

Dadas dos secuencias, encuentre la longitud de la subsecuencia más larga presente en ambas. Una subsecuencia es una secuencia que aparece en el mismo orden relativo, pero no necesariamente contigua. Por ejemplo, “bcd”, “abdg”, “c” son subsecuencias de “abcdefg”.
Aquí hay otra aplicación de programación dinámica. El algoritmo LCS usa DP para resolver el problema desde arriba.
El subproblema actual va a encontrar la subsecuencia común más larga que comienza desde el índice i en la secuencia A, respectivamente desde el índice j en la secuencia B.
A continuación, construiremos la estructura DP lcs[ ][ ] (matriz), donde lcs[ yo][j]es la longitud máxima de una subsecuencia común que comienza desde el índice i en A, respectivamente el índice j en B. Vamos a construirlo de manera descendente. La solución, obviamente, está almacenada en lcs[n][m] , donde n es la longitud de A y m la longitud de B.
La relación de recurrencia es bastante simple e intuitiva. Para simplificar, vamos a considerar que ambas secuencias están indexadas en 1. Primero, vamos a inicializar lcs[i][0] , 1<=i<=n , y lcs[0][j] , 1<=j<=m , con 0, como casos básicos (no hay subsecuencia que parte de 0). Entonces, tomaremos en consideración dos casos principales: si A[i] es igual a B[j] , entonceslcs[i][j] = lcs[i-1][j-1]+1 (un carácter más idéntico que el LCS anterior). En caso contrario, será el máximo entre lcs[i-1][j] (si no se tiene en cuenta A[i] ) y lcs[i][j-1] (si no se tiene en cuenta B[j] ).
Complejidad de tiempo: O(n*m)
Espacio adicional: O(n*m)

Enlaces útiles

Implementación de LCS

9. Subsecuencia creciente más larga

Dada una secuencia A de n elementos, encuentre la longitud de la subsecuencia más larga tal que todos sus elementos estén ordenados en orden creciente. Una subsecuencia es una secuencia que aparece en el mismo orden relativo, pero no necesariamente contigua. Por ejemplo, “bcd”, “abdg”, “c” son subsecuencias de “abcdefg”.
LIS es otro problema clásico que se puede resolver usando Programación Dinámica.
Encontrar la longitud máxima de una subsecuencia creciente se hace usando una matriz l[ ] como estructura de DP, donde l[i] es la longitud máxima de una subsecuencia creciente que contiene A[i] , teniendo sus elementos de [A[i] ], …, A[n]] subsecuencia. l[i] es 1, si todos los elementos después de A[i]son más pequeños que él. De lo contrario, es 1+ como máximo entre todos los elementos después de A[i] que son más grandes que él. Obviamente, l[n]=1 , donde n es la longitud de A. La implementación se realiza de forma ascendente (comenzando desde el final).
Aparece un problema de optimización al buscar el máximo entre todos los elementos después del elemento actual. Lo mejor que podemos hacer es buscar binariamente el elemento máximo.
Para encontrar también una subsecuencia de la longitud máxima ahora conocida, solo tenemos que usar una matriz adicional ind[ ] , que almacena el índice de cada valor máximo.
Complejidad de tiempo: O(n*log n)
Espacio adicional: O(n)

Enlaces útiles

Implementación de LIS

10. Casco convexo

Dado un conjunto de n puntos en el mismo plano, encuentre el polígono convexo de área mínima que contiene todos los puntos dados (situados dentro del polígono o en sus lados). Tal polígono se llama casco convexo. El problema del casco convexo es una geometría clásica que tiene muchas aplicaciones en la vida real. Por ejemplo, la prevención de colisiones: si el casco convexo del automóvil evita las colisiones, el automóvil también lo hace. El cálculo de las rutas se realiza utilizando representaciones convexas de automóviles. El análisis de forma también se realiza con la ayuda de cascos convexos. De esa manera, el procesamiento de imágenes se realiza fácilmente haciendo coincidir los modelos por su árbol de deficiencia convexo.
Se utilizan algunos algoritmos para encontrar el casco convexo, como el algoritmo de Jarvis, el escaneo de Graham, etc. Hoy vamos a hablar sobre el escaneo de Graham y algunas optimizaciones útiles.
El escaneo de Graham clasifica los puntos por su ángulo polar: la pendiente de la línea determinada por un punto determinado y los otros puntos elegidos. Luego, se usa una pila para almacenar el casco convexo en el momento actual. Cuando un punto x se introduce en la pila, otros puntos saldrán de la pila hasta que x y la línea determinada por los dos últimos puntos formen un ángulo inferior a 180°. Finalmente, el último punto introducido en la pila cierra el polígono. Este enfoque tiene una complejidad temporal de O(n*log n) debido a la clasificación. Sin embargo, este método puede producir errores de precisión al calcular la pendiente.
Una solución mejorada que tiene la misma complejidad de tiempo, pero con errores más pequeños, ordena los puntos por sus coordenadas (x, luego y). Luego consideramos la línea formada por los puntos más a la izquierda y más a la derecha y el problema se divide en dos subproblemas. Finalmente, encontramos el casco convexo a cada lado de la línea. El casco convexo de todos los puntos dados es la reunión de los dos cascos.

Enlaces útiles

Implementación de casco convexo

11. Gráficos transversales

El problema de atravesar gráficos se refiere a visitar todos los nodos en un orden particular, generalmente calculando otra información útil en el camino.

Búsqueda primero en amplitud

El algoritmo Breadth-First Search (BFS) es una de las formas más comunes de determinar si un gráfico está conectado o no, o, en otras palabras, para encontrar el componente conectado del nodo fuente del BFS.
BFS también se utiliza para calcular la distancia más corta entre el nodo de origen y todos los demás nodos. Otra versión de BFS es el algoritmo de Lee que se utiliza para calcular el camino más corto entre dos celdas en una cuadrícula.
El algoritmo comienza visitando el nodo de origen y luego sus vecinos que se colocarán en una cola. Se extrae el primer elemento de la cola. Visitaremos a todos sus vecinos y empujaremos a los que no fueron visitados previamente a la cola. El proceso se repite hasta que la cola está vacía. Cuando la cola se vacía, significa que se han visitado todos los vértices alcanzables y el algoritmo finaliza.

Búsqueda en profundidad primero

El algoritmo de búsqueda primero en profundidad (DFS) es otro método transversal común. De hecho, es la mejor opción cuando se trata de verificar la conectividad de un gráfico.
Primero, visitamos el nodo raíz y lo insertamos en una pila. Si bien la pila no está vacía, examinamos el nodo en la parte superior. si el nodo tiene vecinos no visitados, se elige uno de ellos y se coloca en la pila. De lo contrario, si todos sus vecinos han sido visitados, hacemos estallar el nodo. Cuando la pila se vacía, el algoritmo finaliza.
Después de dicho recorrido, se forma un árbol DFS. El árbol DFS tiene muchas aplicaciones; uno de los más comunes es almacenar la hora de “inicio” y “finalización” de cada nodo: el momento en que ingresa a la pila, respectivamente, el momento en que sale de ella.

Enlaces útiles

12. Algoritmo de Floyd-Warshall

El algoritmo de Floyd-Warshall / Roy-Floyd resuelve el problema de la ruta más corta de todos los pares: encuentre las distancias más cortas entre cada par de vértices en un gráfico dirigido ponderado por borde dado.
FW es una aplicación de programación dinámica. La estructura DP (matriz) dist[ ][ ] se inicializa con la matriz gráfica de entrada. Entonces consideramos cada vértice como un intermedio entre otros dos nodos. Los caminos más cortos se actualizan entre cada dos pares de nodos, con cualquier nodo k como vértice intermedio. Si k es un intermedio en la ruta de clasificación entre i y j, dist[i][j] se convierte en el máximo entre dist[i][k]+dist[k][j] y dist[i][j] .
Complejidad temporal: O(n³)
Complejidad espacial: O(n²)

Enlaces útiles

Implementación de FW

13. Algoritmo de Dijkstra y Algoritmo de Bellman-Ford

Algoritmo de Dijkstra

Dado un gráfico y un vértice fuente en el gráfico, encuentra los caminos más cortos desde la fuente hasta todos los vértices en el gráfico dado.
El algoritmo de Dijkstra se usa para encontrar tales caminos en un gráfico ponderado, donde todos los pesos son positivos.
Dijkstra es un algoritmo codicioso que utiliza un árbol de ruta más corta (SPT) con el nodo de origen como raíz. Un SPT es un árbol binario autoequilibrado, pero el algoritmo se puede implementar usando un montón (o una cola de prioridad). Vamos a hablar sobre la solución del montón, porque su complejidad de tiempo es O(|E|*log |V|). La idea es trabajar con una representación de lista de adyacencia del gráfico. De esa forma, los nodos se recorrerán en tiempo O(|V|+|E|) usando BFS.
Todos los vértices se recorren con BFS y aquellos para los que aún no se ha finalizado la distancia más corta se almacenan en un Min-Heap (cola de prioridad).
Se crea el Min-Heap y cada nodo se inserta en él junto con sus valores de distancia. Entonces, la fuente se convierte en la raíz del montón con una distancia de 0. Los otros nodos tendrán infinito asignado como distancia. Si bien el montón no está vacío, extraemos el nodo de valor de distancia mínima x. Para cada vértice y adyacente a x, verificamos si y está en el Min-Heap. En este caso, si el valor de la distancia es mayor que el peso de (x, y) más el valor de la distancia de x, entonces actualizamos el valor de la distancia de y.

Algoritmo Bellman-Ford

Como dijimos anteriormente, Dijkstra solo funciona en gráficos ponderados positivamente. Bellman resuelve este problema. Dado un gráfico ponderado, podemos verificar si contiene un ciclo negativo. Si no, también podemos encontrar las distancias mínimas de nuestra fuente a las demás (pesos negativos posibles).
Bellman-Ford se adapta bien a los sistemas distribuidos, aunque su complejidad temporal es O(|V| |E|).
Inicializamos un dist[ ] como en Dijkstra. Para *|V|-1 veces, para cada borde (x, y) , si dist[y] > dist[x] + peso de (x, y) , entonces actualizamos dist[y] con él.
Repetimos el último paso para encontrar posiblemente un ciclo negativo. La idea es que el último paso garantice la distancia mínima si no hay ciclo negativo. Si hay algún nodo que tiene una distancia más corta en el paso actual que en el último, entonces se detectó un ciclo negativo.

Enlaces útiles

14. Algoritmo de Kruskal

Anteriormente hemos discutido sobre qué es un árbol de expansión mínimo.
Hay dos algoritmos que encuentran el MST de un gráfico: Prim (útil para gráficos densos) y Kruskal (ideal para la mayoría de los gráficos). Ahora vamos a discutir sobre el Algoritmo de Kruskal.
Kruskal ha desarrollado un algoritmo codicioso para encontrar un MST. Es eficiente en grafos raros, porque su complejidad de tiempo es O(|E|*log |V|).
El enfoque del algoritmo es el siguiente: clasificamos todos los bordes en orden creciente de su peso. Luego, se selecciona el borde más pequeño. Si no forma ciclo con el MST actual, lo incluimos. De lo contrario, deséchalo. El último paso se repite hasta que haya aristas |V|-1 en el MST.
La inclusión de aristas en el MST se realiza utilizando Disjoint-Set-Union, también discutido anteriormente.

Enlaces útiles

Implementación Kruskal

15. Clasificación topológica

Un gráfico acíclico dirigido (DAG) es simplemente un gráfico dirigido que no contiene ciclos.
La ordenación topológica en un DAG es una ordenación lineal de vértices tal que para cada arco (x, y) , el nodo x viene antes que el nodo y.
Obviamente, el primer vértice en una ordenación topológica es un vértice con un grado de entrada 0 (no hay arcos que lo dirijan).
Otra propiedad especial es que un DAG no tiene una clasificación topológica única.
La implementación de BFS sigue esta rutina: se encuentra un nodo con un grado de entrada 0 y se empuja el primero a la clasificación. Este vértice se elimina del gráfico. Como el nuevo gráfico también es un DAG, podemos repetir el proceso.

En cualquier momento durante DFS, un nodo puede estar en una de estas tres categorías:

nodos que terminamos de visitar (sacados de la pila);
nodos que están actualmente en la pila;
nodos que aún no se han descubierto.

Si durante DFS en un DAG un nodo x tiene un borde saliente a un nodo y, entonces y está en la primera o en la tercera categoría. Si y estuviera en la pila, entonces (x, y) terminaría un ciclo, hecho que contradice la definición de DAG.
Esta propiedad en realidad nos dice que se extrae un vértice de la pila después de que se extraen todos sus vecinos salientes. Entonces, para clasificar topológicamente un gráfico, debemos realizar un seguimiento de una lista de orden inverso de los vértices reventados.

Enlaces útiles

Implementación de clasificación topológica

Deja tus comentarios y sugerencias

Sobre Facialix

Facialix es un sitio web que tiene como objetivo apoyar en el aprendizaje y educación de jóvenes y grandes. Buscando y categorizando recursos educativos gratuitos de internet, de esta manera Facialix ayuda en el constante aprendizaje de todos.